【Algorithm】P、NP、NPC和NP-Hard问题
目录
先用几句话简单说明一下时间复杂度。**时间复杂度并不是表示一个程序解决问题需要花多少时间,而是当问题规模扩大后,程序运行需要的时间增长得有多快。**也就是说,对于高速处理数据的计算机来说,处理某一个特定数据的效率不能衡量一个程序的好坏,而应该看当这个数据的规模变大到数百倍后,程序运行时间是否还是一样,或者也跟着慢了数百倍,或者变慢了数万倍。不管数据有多大,程序处理花的时间始终是一样的,我们就说这个程序很好,具有 $O(1)$ 的时间复杂度,也称常数级复杂度;数据规模变得有多大,花的时间也跟着变得有多长,这个程序的时间复杂度就是 $O(n)$,比如找 $n$ 个数中的最大值;而像冒泡排序、插入排序等,数据扩大 $2$ 倍,时间变慢 $4$ 倍的,属于 $O(n^2)$ 的复杂度。还有一些穷举类的算法,所需时间长度成几何阶数上涨,这就是 $O(a^n)$ 的指数级复杂度,甚至 $O(n!)$ 的阶乘级复杂度。不会存在 $O(2n^2)$ 的复杂度,因为前面的那个 $2$ 是系数,根本不会影响到整个程序的时间增长。同样地,$O (n^3+n^2)$ 的复杂度也就是 $O(n^3)$ 的复杂度。因此,我们会说,一个 $O(0.01n^3)$ 的程序的效率比 $O(100n^2)$ 的效率低,尽管在 $n$ 很小的时候,前者优于后者,但后者运行所需的时间随数据规模增长得慢,最终 $O(n^3)$ 的复杂度将远远超过 $O(n^2)$。我们也说,$O(n^{100})$ 的复杂度小于 $O(1.01^n)$ 的复杂度。
容易看出,前面的几类复杂度被分为两种级别,其中后者的复杂度无论如何都远远大于前者:一种是 $O(1),O(log(n)),O(n^a)$ 等,我们把它叫做多项式级的复杂度,因为它的规模 $n$ 出现在底数的位置;另一种是 $O(a^n)$ 和 $O(n!)$ 型复杂度,它是非多项式级的,其复杂度计算机往往不能承受。当我们在解决一个问题时,我们选择的算法通常都需要是多项式级的复杂度,非多项式级的复杂度需要的时间太多,往往会超时,除非是数据规模非常小。
自然地,人们会想到一个问题:会不会所有的问题都可以找到复杂度为多项式级的算法呢?很遗憾,答案是否定的。有些问题甚至根本不可能找到一个正确的算法,这称之为“不可解问题”(Undecidable Decision Problem)。 Halting Problem 就是一个著名的不可解问题。再比如,输出从 $1$ 到 $n$ 这 $n$ 个数的全排列。不管你用什么方法,你的复杂度都是阶乘级,因为你总得用阶乘级的时间打印出结果来。有人说,这样的“问题”不是一个“正规”的问题,正规的问题是让程序解决一个问题,输出一个“YES”或“NO”(这被称为判定性问题),或者一个什么什么的最优值(这被称为最优化问题)。那么,根据这个定义,也能举出一个不大可能会有多项式级算法的问题来:Hamilton 回路。问题是这样的:给你一个图,问你能否找到一条经过每个顶点一次且恰好一次(不遗漏也不重复)最后又走回来的路(满足这个条件的路径叫做 Hamilton 回路)。这个问题现在还没有找到多项式级的算法。事实上,这个问题就是我们后面要说的 NPC 问题。
下面引入 P 类问题的概念:**如果一个问题可以找到一个能在多项式的时间里解决它的算法,那么这个问题就属于 P 问题,P 是英文单词多项式(Polynomial )的第一个字母。**哪些问题是 P 类问题呢?比如排序一个数组,判断一个数是否是质数,判断一个图是否是二分图,这些问题都是 P 类问题。
接下来引入 NP 问题的概念。这个就有点难理解了,或者说容易理解错误。在这里强调,NP 问题不是非 P 类问题,也就是说 NP 代表的不是 Non-Polynomial,而是 Nondeterministic Polynomial,指的是非确定性图灵机下的多项式时间,核心在于验证而不是解决。什么意思呢?就是说 NP 问题是指可以在多项式的时间里验证一个解的问题。**NP 问题的另一个定义是,可以在多项式的时间里猜出一个解的问题。**比方说,我运气很好,在程序中需要枚举时,我可以一猜一个准。现在某人拿到了一个求最短路径的问题,问从起点到终点是否有一条小于 $100$ 个单位长度的路线。它根据数据画好了图,但怎么也算不出来,于是来问我:你看怎么选条路走得最少?我说,我运气很好,肯定能随便给你指条很短的路出来。然后我就胡乱画了几条线,说就这条吧。那人按我指的这条路把权值加起来一看,嘿,神了,路径长度 $98$,比 $100$ 小。于是答案出来了,存在比 $100$ 小的路径。别人会问他这题怎么做出来的,他就可以说,因为我找到了一个比 $100$ 小的解。在这个题中,找一个解很困难,但验证一个解很容易。验证一个解只需要 $O(n)$ 的时间复杂度,也就是说我可以花 $O(n)$ 的时间把我猜的路径的长度加出来。这就是可以在多项式时间里验证解的一个问题,但是不一定能够在多项式时间里解决这个问题,这就是 NP 问题。当然有不是 NP 问题的问题,即你猜到了解但是没用,因为你不能在多项式的时间里去验证它。下面我要举的例子是一个经典的例子,它指出了一个目前还没有办法在多项式的时间里验证一个解的问题。很显然,前面所说的 Hamilton 回路是 NP 问题,因为验证一条路是否恰好经过了每一个顶点非常容易。但我要把问题换成这样:试问一个图中是否存在 Hamilton 回路。这样问题就没法在多项式的时间里进行验证了,因为除非你试过所有的路,否则你不敢断定它“没有 Hamilton 回路”。
之所以要定义 NP 问题,是因为通常只有 NP 问题才可能找到多项式的算法。我们不会指望一个连多项式地验证一个解都不行的问题存在一个解决它的多项式级的算法。相信读者很快明白,信息学中的号称最困难的问题——“NP 问题”,实际上是在探讨 NP 问题与 P 类问题的关系。
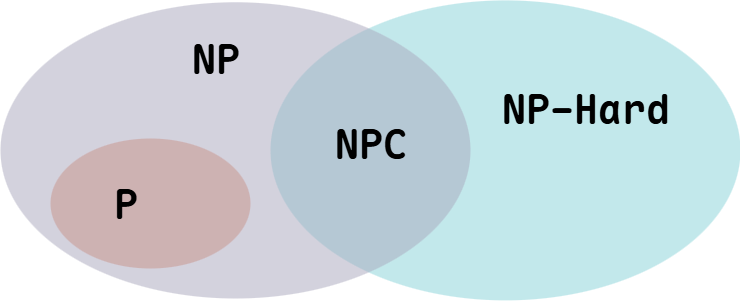
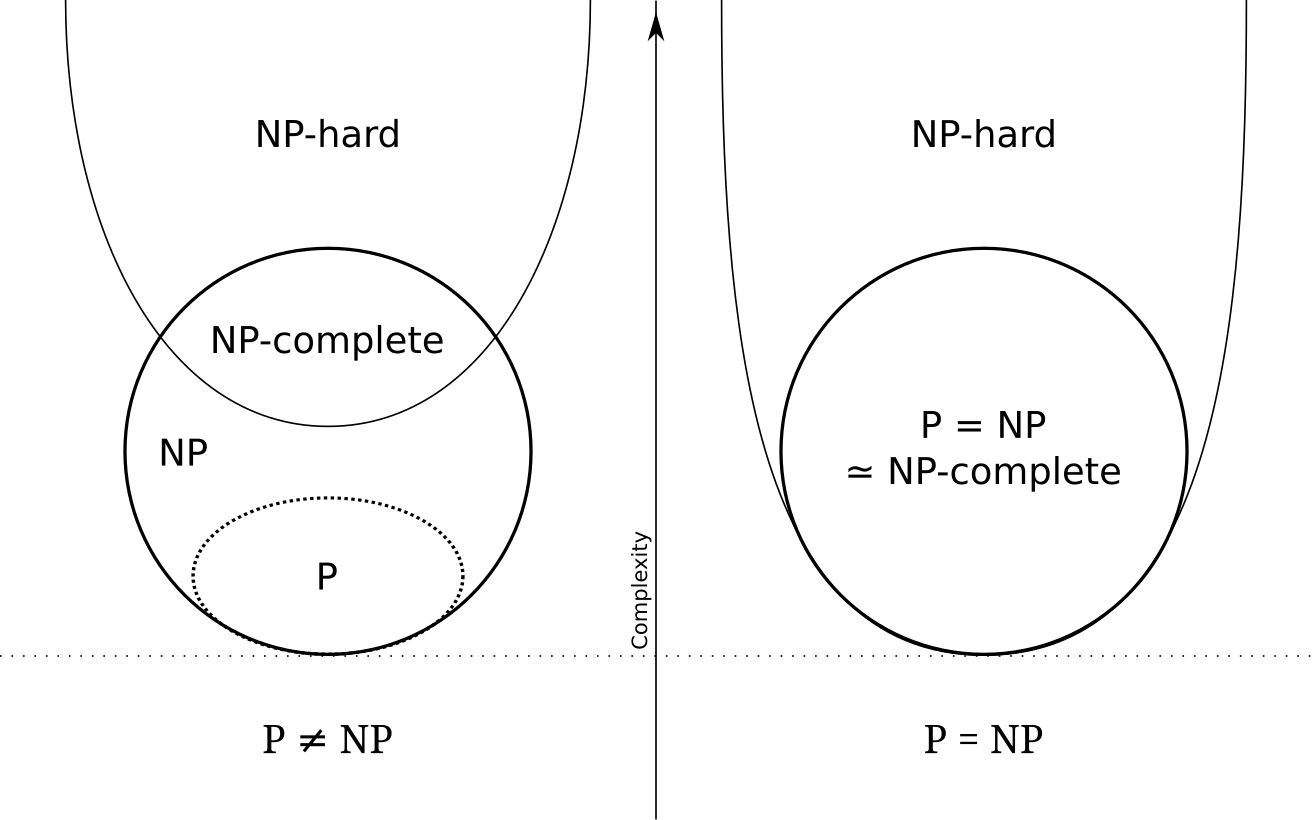
很显然,所有的 P 类问题都是 NP 问题。也就是说,能多项式地解决一个问题,必然能多项式地验证一个问题的解——既然正解都出来了,验证任意给定的解也只需要比较一下就可以了。关键是,人们想知道,是否所有的 NP 问题都是 P 类问题。我们可以再用集合的观点来说明,如果把所有 P 类问题归为一个集合 P 中,把所有 NP 问题划进另一个集合 NP 中,那么,显然有 P 属于 NP。现在,所有对 NP 问题的研究都集中在一个问题上,即究竟是否有 P=NP?通常所谓的“NP 问题”,其实就一句话:证明或推翻 P=NP。
NP 问题一直都是信息学的巅峰。巅峰,意即很引人注目但难以解决。在信息学研究中,这是一个耗费了很多时间和精力也没有解决的终极问题,好比物理学中的大统一和数学中的歌德巴赫猜想等。
目前为止这个问题还“啃不动”。但是,一个总的趋势、一个大方向是有的。人们普遍认为,P=NP 不成立,也就是说,多数人相信,存在至少一个不可能有多项式级复杂度的算法的 NP 问题。人们如此坚信 P≠NP 是有原因的,就是在研究 NP 问题的过程中找出了一类非常特殊的 NP 问题叫做 NP-完全(NP-Complete)问题,也即所谓的 NPC 问题。正是 NPC 问题的存在,使人们相信 P≠NP。下文将花大量篇幅介绍 NPC 问题,你从中可以体会到 NPC 问题的存在使 P=NP 变得多么不可思议。
为了说明 NPC 问题,我们先引入一个概念——约化(Reducibility,有的资料上叫“归约”)。
简单地说,一个问题 A 可以约化为问题 B 的含义即是,可以用问题 B 的解法解决问题 A,或者说,问题 A 可以“变成”问题 B。 《算法导论》上举了这么一个例子。比如说,现在有两个问题:求解一个一元一次方程和求解一个一元二次方程。那么我们说,前者可以约化为后者,意即知道如何解一个一元二次方程那么一定能解出一元一次方程。我们可以写出两个程序分别对应两个问题,那么我们能找到一个“规则”,按照这个规则把解一元一次方程程序的输入数据变一下,用在解一元二次方程的程序上,两个程序总能得到一样的结果。这个规则即是:两个方程的对应项系数不变,一元二次方程的二次项系数为 $0$。按照这个规则把前一个问题转换成后一个问题,两个问题就等价了。同样地,我们可以说,Hamilton 回路可以约化为 TSP(Travelling Salesman Problem,旅行商问题):在 Hamilton 回路问题中,两点相连即这两点距离为 $0$,两点不直接相连则令其距离为 $1$,于是问题转化为在 TSP 中,是否存在一条长为 $0$ 的路径。Hamilton 回路存在当且仅当 TSP 中存在长为 $0$ 的回路。
“问题 A 可约化为问题 B”有一个重要的直观意义:B 的时间复杂度高于或者等于 A 的时间复杂度。也就是说,问题 A 不比问题 B 难。这很容易理解。既然问题 A 能用问题 B 来解决,倘若 B 的时间复杂度比 A 的时间复杂度还低了,那 A 的算法就可以改进为 B 的算法,两者的时间复杂度还是相同。正如解一元二次方程比解一元一次方程难,因为解决前者的方法可以用来解决后者。
很显然,约化具有一项重要的性质:约化具有传递性。如果问题 A 可约化为问题 B,问题 B 可约化为问题 C,则问题 A 一定可约化为问题 C。这个道理非常简单,就不必阐述了。
现在再来说一下约化的标准概念就不难理解了:如果能找到这样一个变化法则,对任意一个程序 A 的输入,都能按这个法则变换成程序 B 的输入,使两程序的输出相同,那么我们说,问题 A 可约化为问题 B 。当然,我们所说的“可约化”是指的可“多项式地”约化(Polynomial-time Reducible),即变换输入的方法是能在多项式的时间里完成的。约化的过程只有用多项式的时间完成才有意义。
好了,从约化的定义中我们看到,一个问题约化为另一个问题,时间复杂度增加了(也可能没有增加),问题的应用范围也增大了。通过对某些问题的不断约化,我们能够不断寻找复杂度更高,但应用范围更广的算法来代替复杂度虽然低,但只能用于很小的一类问题的算法。再回想前面讲的 P 和 NP 问题,联想起约化的传递性,自然地,我们会想问,如果不断地约化上去,不断找到能“通吃”若干小 NP 问题的一个稍复杂的大 NP 问题,那么最后是否有可能找到一个时间复杂度最高,并且能“通吃”所有的 NP 问题的这样一个超级 NP 问题?答案居然是肯定的。也就是说,存在这样一个 NP 问题,所有的 NP 问题都可以约化成它。换句话说,只要解决了这个问题,那么所有的 NP 问题都解决了。这种问题的存在难以置信,并且更加不可思议的是,这种问题不只一个,它有很多个,它是一类问题。这一类问题就是传说中的 NPC 问题,也就是 NP-Complete 问题。NPC 问题的出现使整个 NP 问题的研究得到了飞跃式的发展。我们有理由相信,NPC 问题是最复杂的问题。我们可以看到,人们想表达一个问题不存在多项式的高效算法时应该说它“属于 NPC 问题”,而不是说它“属于 NP 问题”。此时,我的目的终于达到了,我已经把 NP 问题和 NPC 问题区别开了。
NPC 问题的定义非常简单。同时满足下面两个条件的问题就是 NPC 问题。**首先,它得是一个 NP 问题;然后,所有的 NP 问题都可以在多项式时间内约化到它。**证明一个问题是 NPC 问题也很简单。先证明它至少是一个 NP 问题,再证明其中一个已知的 NPC 问题能约化到它(由约化的传递性,则 NPC 问题定义的第二条也得以满足;至于第一个 NPC 问题是怎么来的,下文将介绍),这样就可以说它是 NPC 问题了。
既然所有的 NP 问题都能约化成 NPC 问题,那么只要任意一个 NPC 问题找到了一个多项式的算法,那么所有的 NP 问题都能用这个算法解决了,NP 也就等于 P 了。因此,给 NPC 找一个多项式算法太不可思议了。因此,前文才说,“正是 NPC 问题的存在,使人们相信 P≠NP”。我们可以就此直观地理解,NPC 问题目前没有多项式的有效算法,只能用指数级甚至阶乘级复杂度的搜索。
顺便讲一下 NP-Hard 问题。NP-Hard 问题是这样一种问题,它满足 NPC 问题定义的第二条但不一定要满足第一条(就是说,NP-Hard 问题要比 NPC 问题的范围广)。NP-Hard 问题同样难以找到多项式的算法,但它不一定是 NP 问题。即使 NPC 问题发现了多项式级的算法,NP-Hard 问题有可能仍然无法得到多项式级的算法。事实上,由于 NP-Hard 放宽了限定条件,它将有可能比所有的 NPC 问题的时间复杂度更高从而更难以解决。
接下来讲一下第一个 NPC 问题是怎么来的,第一个 NPC 问题叫做 Boolean satisfiability problem(或者叫做 propositional satisfiability problem,缩写 SAT 或 B-SAT)。它是这样一种问题:给定一个逻辑电路,问是否存在一种输入使输出为 True。什么叫做逻辑电路呢?一个逻辑电路由若干个输入,一个输出,若干“逻辑门”和密密麻麻的线组成。比如对于逻辑电路 “$a$ AND NOT $b$” 来说,我们可以找到 $a$ = True 和 $b$ = False 使得输出为 True,相反,对于逻辑电路 “$a$ AND NOT $a$” 来说,我们找不到一个输入使得输出为 True。
B-SAT 属于 NPC 问题。这是有严格证明的,感兴趣的可以查阅 Cook–Levin theorem。它显然属于 NP 问题,并且可以直接证明所有的 NP 问题都可以约化到它(不要以为 NP 问题有无穷多个将给证明造成不可逾越的困难)。证明过程相当复杂,其大概意思是说任意一个 NP 问题的输入和输出都可以转换成逻辑电路的输入和输出(想想计算机内部也不过是一些 $0$ 和 $1$ 的运算),因此对于一个 NP 问题来说,问题转化为了求出满足结果为 True 的一个输入(即一个可行解)。
有了第一个 NPC 问题后,一大堆 NPC 问题就出现了,因为再证明一个新的 NPC 问题只需要将一个已知的 NPC 问题约化到它就行了。后来,Hamilton 回路成了 NPC 问题,TSP 也成了 NPC 问题。现在被证明是 NPC 问题的有很多,任何一个找到了多项式算法的话所有的 NP 问题都可以完美解决了。因此说,正是因为 NPC 问题的存在,P=NP 变得难以置信。
总结一下,对于 P、NP 和 NPC 问题,这些概念讨论的都是决策问题,即答案是“是”或“否”的问题(例如:是否存在一条长度小于 K 的路径?这个公式是否可满足?)。
P 类问题是包含所有可以在多项式时间内被 确定型图灵机(Deterministic Turing machine,可以简单理解为常规计算机上的确定性算法)解决的决策问题。
NP 类问题(nondeterministic polynomial time)是包含所有可以在多项式时间内被确定型图灵机验证一个给定解的决策问题,另外一个定义是包含所有可以在多项式时间内被 非确定型图灵机(Nondeterministic Turing machine)解决的决策问题。所以 NP 类问题的 N 不是表示“非”的意思,而是来源于非确定型图灵机的 Nondeterministic,不要混淆非 P 类问题和 NP 类问题。如果将 NP 类问题理解为非 P 类问题会使得 P=NP 问题是世界级难题(P=NP 问题是克雷数学研究所悬赏百万美元的七个“千禧年大奖难题”之一,其他问题可以在 The Millennium Prize Problems 这里找到)变成一个笑话。
一个问题是 NP-Complete(NPC 或者 NP-C)问题当且仅当它满足两个条件,这个问题本身属于 NP 类问题,NP 类问题中的每一个问题都可以在多项式时间内归约(reduce)到这个问题。第一个 NPC 问题是 B-SAT,它是由 Cook–Levin theorem 证明的,其他 NPC 问题则是由 B-SAT 问题归约证明为 NPC 问题。
一个问题是 NP-Hard 类问题当且仅当它满足 NP 中的每一个问题都可以在多项式时间内归约到这个问题,和 NPC 类问题的区别在于,NP-Hard 类问题不要求它本身是一个 NP 问题。NP-Hard 问题不一定是决策问题,也不一定能在多项式时间内验证一个解 ,只要求所有的 NP 问题都能归约到它。NP-Hard 问题至少和 NP 问题一样难,如果一个 NP-Hard 问题存在多项式时间算法,那么所有 NP 问题(包括 NPC)都存在多项式时间算法(P=NP)。反之,如果 P ≠ NP,那么任何 NP-Hard 问题都不存在多项式时间算法。NP-Hard 类包含所有 NP-Complete 问题(因为 NPC 问题满足归约要求且属于 NP),但也包含那些不属于 NP 的、甚至更难的问题。属于非决策问题的 NP-Hard 问题:许多经典的优化问题(求最大值、最小值)的决策版本是 NPC,但它们的优化版本本身通常被认为是 NP-Hard(因为它们通常比决策版本更难或等价),比如 TSP 和 B-SAT(所有的 NPC 问题)、停机问题( Halting Problem)、旅行商问题的优化版本(求访问所有城市的最短回路长度)和判定一个围棋或国际象棋位置是否必胜。
所以当我们以后遇到一个实际问题,如果在一般情况下(对于所有可能的输入),不存在已知的、对所有输入都高效(多项式时间)的精确求解算法,我们应该说这个问题是 NPC 或者是 NP-Hard 的,而不是 NP。不能用精确求解算法的情况下,一般有这几种解决方法:小规模输入(回溯和分支定界等)采用精确算法,近似算法(在多项式时间内找到不一定最优但质量有保证的解),启发式算法(在多项式时间内找到通常较好但不保证质量的解,如贪心、局部搜索、遗传算法)和随机算法(利用随机性,有时能快速找到解或以高概率找到好解,如 Monte Carlo 算法)。
参考资料
- 什么是P问题、NP问题和NPC问题 | Matrix67: The Aha Moments 写得很好的一篇辨析文章,本文大部分也是参考这篇文章得到的